Because a picture is worth a thousand words

Linear Search​

A linear search is the most basic search algorithm. It iterates through a list sequentially from the first to the last index. At each index, it fetches the value and checks if it matches the search query.

Time Complexity of Linear Search​

The average search time for a linear search increases linearly with the size of the list—hence the name linear search.

• If the execution time is T for a list with N elements, then:
  • A list with 2N elements takes 2T time.
  • A list with 3N elements takes 3T time.
  • And so on.

Visualizing Linear Search​

The following graph represents the time taken to search a list using linear search. Each sample was searched only once to record search time.

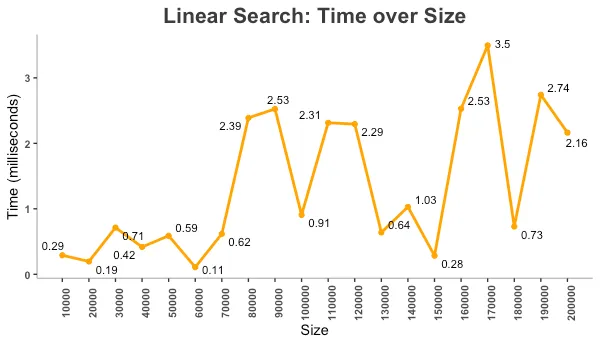
The graph is not a straight line because search time is affected by factors beyond our control, such as:

• Memory allocation
• CPU allocation
• Position of the searched item in the list

If the searched item is the first element, linear search finds it instantly.
If the item is not in the list, or is the last element, the search takes N steps (where N is the list size).

---

To eliminate randomness, we increase the number of search iterations .
Repeating the search multiple times averages out external influences, revealing a more linear pattern.

Search Time Over Multiple Iterations​

We conduct linear search 10, 100, and 1000 times and observe the trends:

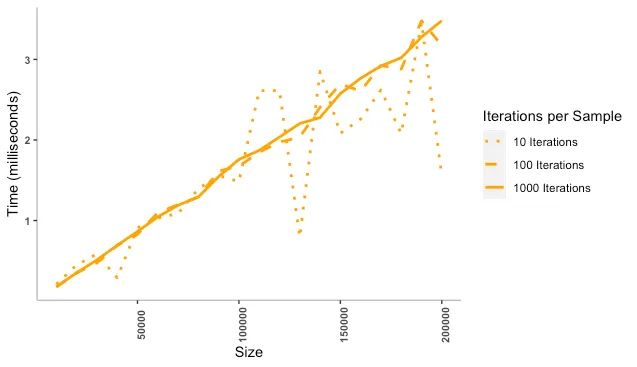
As we can see, the effects of randomness diminish with multiple searches, resulting in a plot that approaches a straight line.

---

Linear Search Complexity​

We now run 1000 iterations per sample size to confirm the linear relationship.

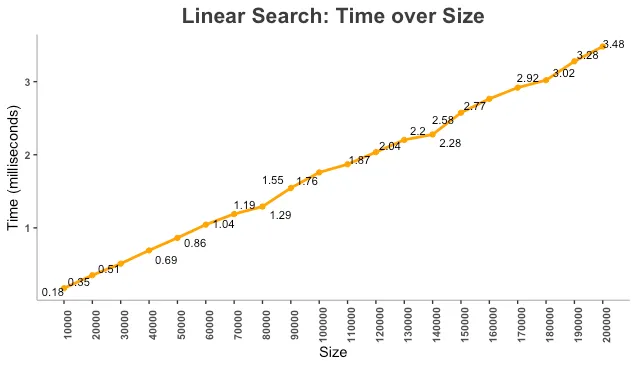
Observations:

• For 10,000 elements → Average search time 0.18 ms
• For 20,000 elements → Search time 0.35 ms (approximately double)
• For 100,000 elements → Search time 1.76 ms (approximately 10x the initial size)

This confirms that linear search execution time grows proportionally with list size → Time Complexity: O(N).

---

Binary Search

Binary Search is a more efficient searching algorithm that only works for sorted lists.

It repeatedly divides the search interval in half, eliminating half of the remaining elements in each step.

Visualizing Binary Search​

Following is the graph of a list being searched using the binary search algorithm.

Each sample size was searched 10,000 times to record the search time.

Unlike linear search, binary search has an O(log N) complexity.

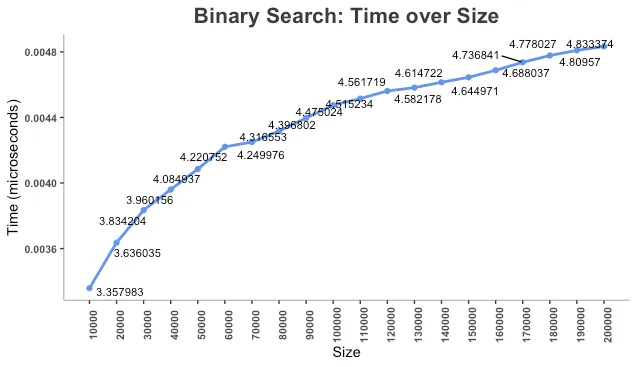
Unlike the clear linear relationship in linear search, the logarithmic nature of binary search is not as visually obvious.

Mathematical Proof: O(log N) Complexity​

Theoretically, it can be proven that for the binary search the time complexity is O(Log N) i.e the search time is proportional to the log of list size

$T(N) = O(\log N)$

Using an initial search time of 3.358 µs for 10,000 elements, we calculate:

• For 20,000 elements:

  $3.358 \times \left( \log(20000) \div \log(10000) \right) = 3.61 \text{ microseconds}$

• For 30,000 elements: $3.358 \times \left( \log(30000) \div \log(10000) \right) = 3.75 \text{ microseconds}$

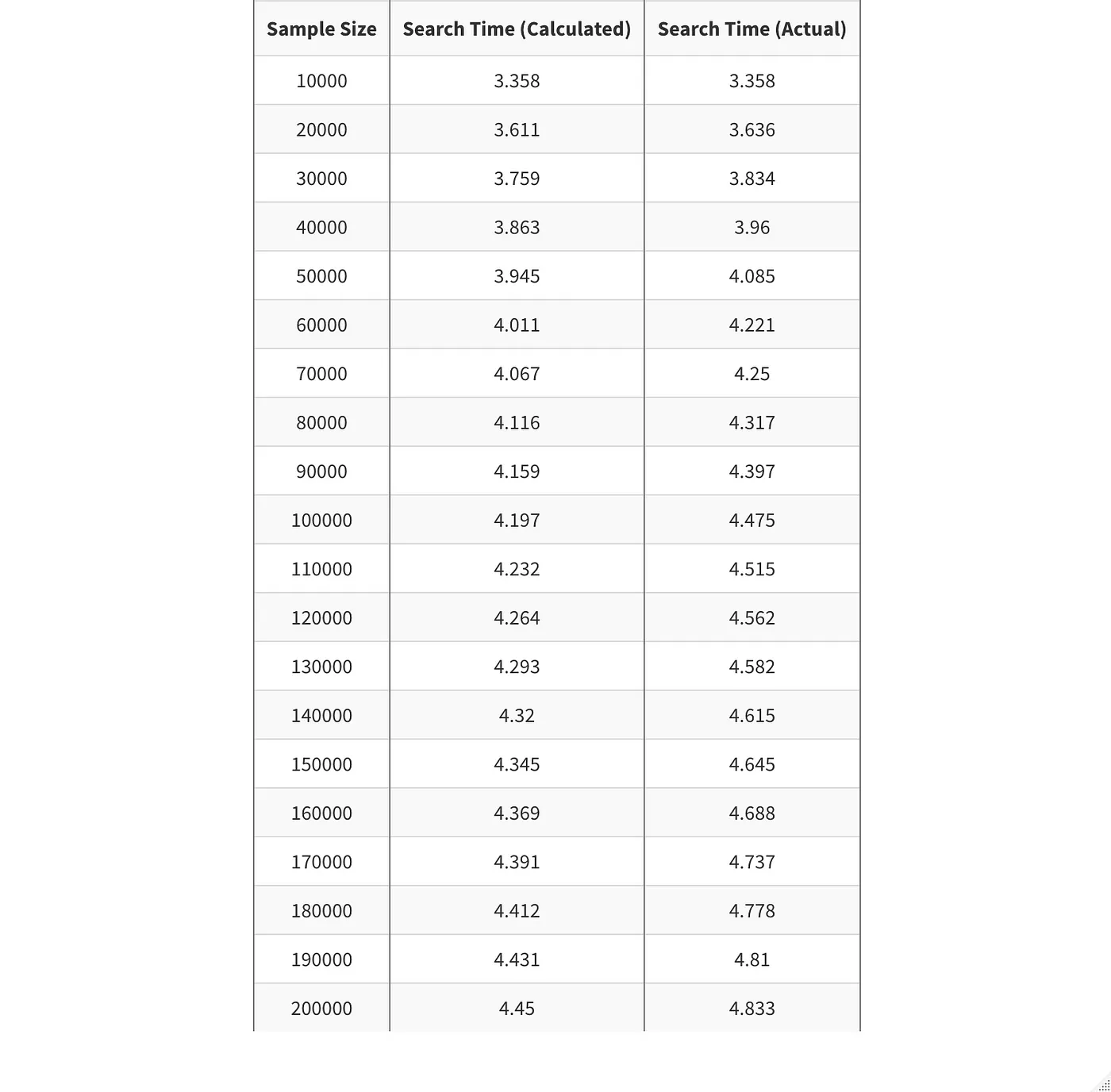
Expected vs. Actual Search Times

The table below compares calculated vs. actual search times:

---

Linear Search vs. Binary Search

Finally, let's compare the search times of linear search and binary search:

💡 Observations:

• Linear search times increase significantly as list size grows.
• Binary search times remain almost constant due to its logarithmic nature.
• The difference is barely noticeable for small lists but becomes drastic for larger lists.

---

Linear Search in an Ordered List​

Unlike binary search, linear search does not require sorting beforehand.

But does ordering the list affect the performance of linear search?

I expected no difference, but the results were surprising!

Searching an ordered list took longer than searching an unordered list.

Why Does Sorting Affect Search Time?​

I am not sure but, one possible explanation is:

• The searched values (randomly generated) tend to fall in the upper range.
• In an ordered list, linear search needs to traverse at least N/2 elements.

Any of these can results in higher average search times for an sorted list compared to an unsorted list.

---

Key Takeaways​

• Linear Search** is O(N) and works on unsorted lists.
• Binary Search** is O(log N) but requires sorted data.
• Binary search outperforms linear search** for large lists.
• Sorting a list affects linear search performance in unexpected ways.

Final Thought

Both algorithms have their use cases—linear search for small lists and binary search for large, sorted lists.
Choosing the right search method depends on the dataset and constraints.

---

Thank You!

Hope you enjoyed this article! If you have questions, suggestions, or corrections, feel free to comment below.

🚀 Stay tuned for more insights into algorithms and performance analysis!